이상치(outlier)는 데이터 세트에서 평균과 표준편차 같은 통계량(statistics)에 왜곡된 결과를 낸다. 그렇기 때문에 통계에서 IQR(Interquartile Range) 이상치 판별법 같은 이상치(outlier)를 판별하기 위한 방법들이 이용되고 있다.
환율 데이터에도 1997~2021/04 사이에 IQR(Interquartile Range) 이상치 판별법을 사용해서 이상치(outlier)를 검출해보고, 이상치(outlier)를 제외한 데이터의 평균과 표준편차를 비교해본다.
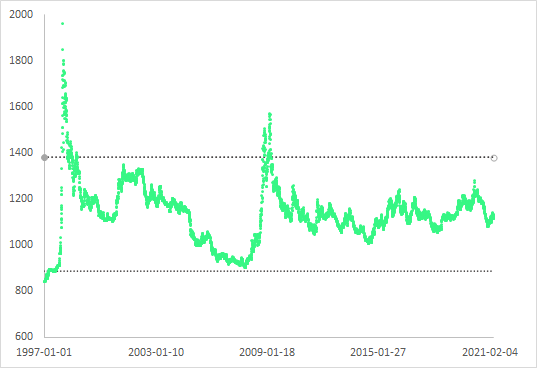
그리고 데이터를 고급 필터 기능을 이용해서 임의의 구간으로 데이터를 나누고 파이 차트(pie chart)를 그려서 정리해본다.
이상치(Outlier) 찾기
환율 데이터에 이상치(outlier)로 의심되는 값들이 1997년 외환위기, 2008 리만브라더스 경제 위기를 전후로 해서 집중돼있다. IQR를 이용해서 이상치 값을 찾아본다.
1단계: IQR구하기
우선 Q1, Q3를 찾아서 Q3-Q1 = IQR 찾는다.
2단계: 상한 값, 하한값 구하기
Q3값에서 IQR에 1.5배 더 위에 값을 상한값, Q1값에서 IQR에 1.5배 더 먼 아래에 값을 하한 값으로 지정하고 경계선 밖에 값을 이상치(outlier)로 둔다.

3단계: 이상치 검정하기
위에서 구한 이상치(outlier)를 그럽스 검정(Grubb's test)을 통해서 이상치(outlier) 판별을 통해서 검정해본다.
우선 정규분포(normal distribution)에 근사하는지 확인한다.
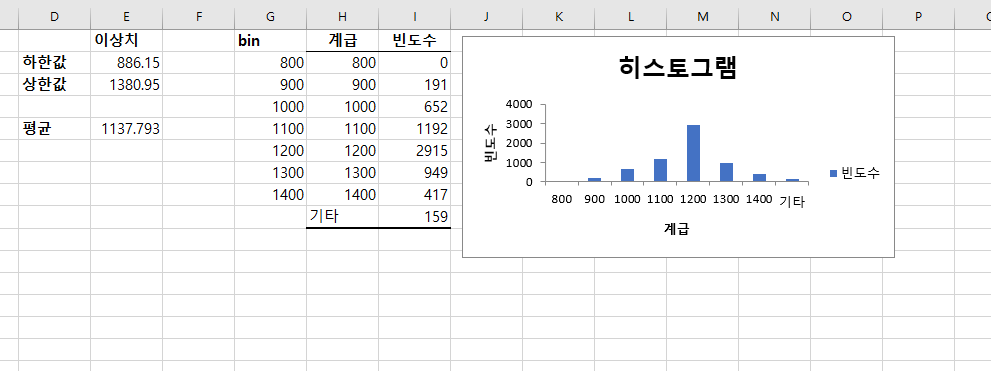
평균 1137.793이고 1200측에서 히스토그램이 가장 높게 나타내고 양측으로 갈수록 대칭적으로 감소하는 종 모양 분포(bell-shaped distribution)를 취하고 있다.
그럽스 검정(Grubbs' test)을 상한 이상치에 대해서 적용해본다.
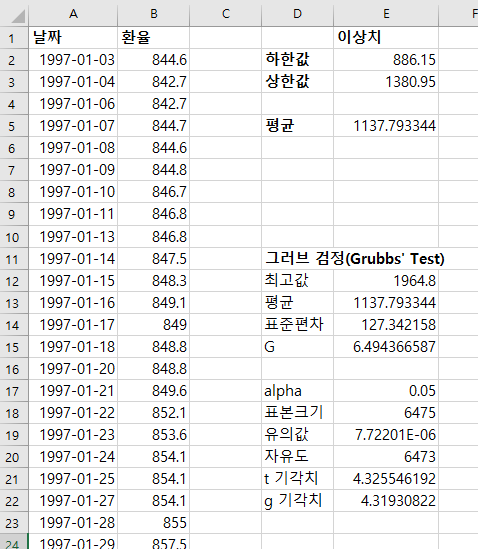
최고값 1964.8은 이상치의 g 통계량은 6.494, g 기각치는 4.3193이다. g 통계량이 기각치보다 크기 때문에 1380.95는 이상치(ouliter)로 판별한다.
하한값 이상치에도 위와 같이 적용한다.

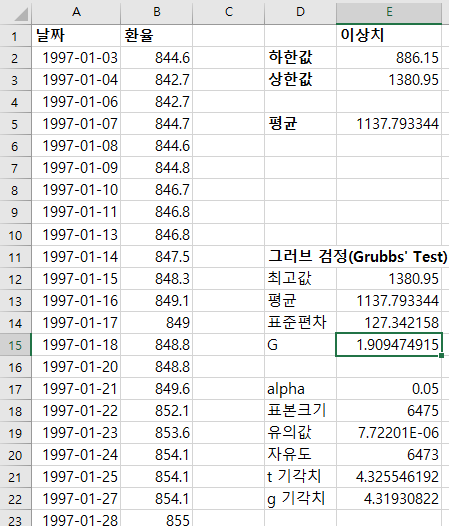
IQR 법으로 구한 이상치 하한값 886.15, 상한값 1380.95를 하면 g값은 2.317, 1.909로 기각치 4.3193보다 작기 때문에 이상치(outlier)로 판별되지 않는다.
여기서는 IQR 법으로 구한 이상치(outlier) 값을 이상치로 분류하고 분석한다. 왜냐하면 실제 관찰 기록을 적용해서 판별해보면 환율 1300, 환율 800원은 특이값이기 때문이다.
4단계: 이상치 판별

구한 하한 값(lower limit), 상한 값(upper limit)을 가지고 하한 값보다 작거나, 상한 값보다 크다면 이상치로 '1', 아니면 '0'이 나오게 조건을 주어 전체 셀에 적용한다.
4단계: 이상치 '1'을 데이터 고급 필터 기능을 이용해서 분류한다.
고급 필터에서 이상치 판별 1에 조건을 입력하고 다른 위치에 필터 결과를 출력한다.
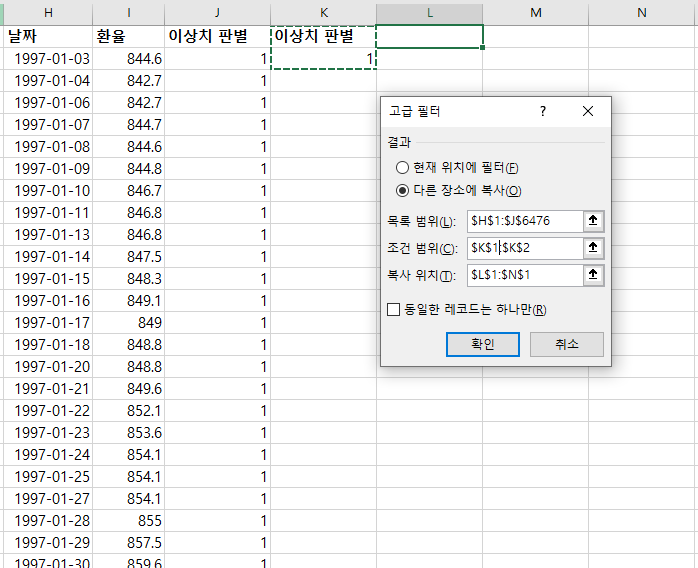
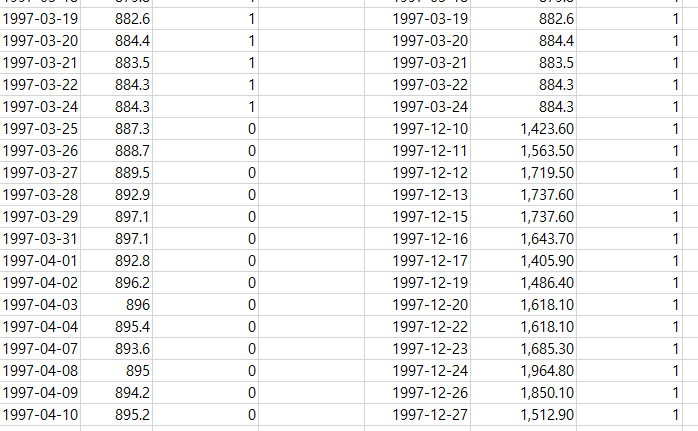
이상치가 1인 데이터만 필터 돼서 새로 만들어진다.

...
파이 차트(pie chart) 그리기
다음으로 파이 차트(pie chart)를 그려본다. 전체 데이터에서 임의로 지정한 구간들에 대한 조건값을 입력한다.

데이터를 선택하고, 삽입 > 차트 > 원형 또는 도넛형 차트 삽입에 들어간다.
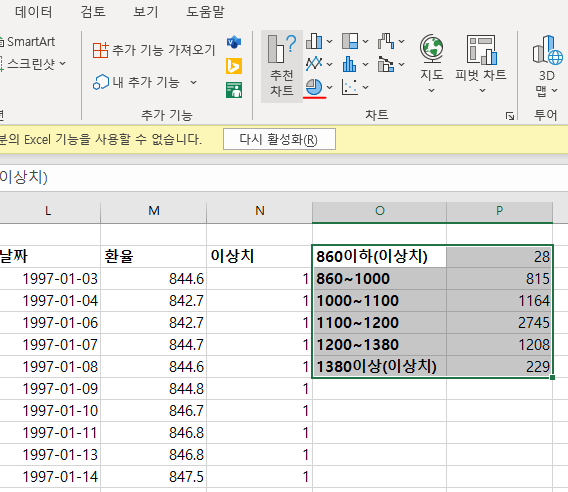
2차원 차트 원형 차트를 선택한다.

파이 차트(pie chart)가 나온다. 이제 원하는 모양대로 보기 좋게 수정한다.

환율에서 이상치가 차지하는 비중은 4%, 860~1000원 때 기간은 13%, 1000~1100원은 19%, 1100~1200원 때는 44%, 1200~1380원 때는 20% 였다. 이에 환율은 작게는 1000~1200 때에서 44%+19% = 63% 로 과반수 이상을 차지했다.
※ 관련 포스팅
엑셀에서 IQR(Interquartile Range) 구하기
엑셀에서 분산형 그래프(Scatterplot)에 구분선 추가하기
'Excel_데이터 > 실전 데이터 분석: 환율' 카테고리의 다른 글
| 환율 최솟값, Q1, Q3, 중간값, 최댓값 구하고 상자그림(box plot) 그려보기 (0) | 2021.04.13 |
|---|