회귀분석에서 두 개 이상의 원인 변수(explanatory variables)가 있을 때, 서로의 원인 변수(explanatory variables)가 서로 가깝게 관계되어있는 정도를 다중 공산성(Multicollinearity)이라고 한다.
다중 공산성(Multicollinearity)이 발생하면 결과(y-값)에 주요하게 영향을 미치는 원인 변수(explanatory variable)를 선정하기 어려운 문제가 발생한다. 그래서 회귀분석을 할 때 문제가 생긴다.
두 개 이상의 원인 변수(explanatory variables)에 다중 공산성(Multicollinearity)을 판별하는 방법이 필요하다. 그때 사용하는 방법 분산 팽창 계수(VIF)이다.
분산 팽창 계수(VIF)는 두 변수 간에 상관성(corrleation)과 상관성 정도를 측정한다.
이번 포스팅에서 엑셀에서 분산 팽창 계수(VIF)를 구해본다.
예시: 엑셀에서 분산 팽창 계수(VIF) 구하기
아래에 10명의 농구 선수들에 점수, 득점, 도움, 리바운드 기록이 있다. 여기서 점수를 반응 변수(reponse variable), 득점, 도움, 리바운드를 원인 변수(explanatory variable)로 하여 다중 회귀분석(Mutiple linear regression)을 한다.

1단계: 다중 회귀분석(multiple linear regression)을 한다.
데이터 분석 툴에 들어가서 데이터 분석을 한다.

데이터 분석이 없다면 여기서 다운 받는다.
데이터 분석을 클릭하고 회귀분석을 선택한다.

분석 창에 칸을 아래와 같이 채워 넣는다.
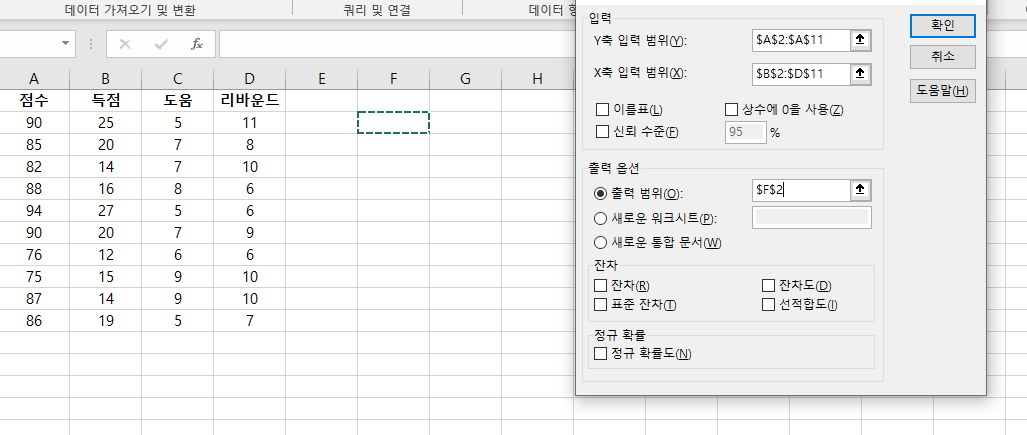
그러면 이와 같은 결과가 프린트된다.

2단계: 각 원인 변수(explanatory variable) 별로 VIF를 계산한다.
3개의 각 원인 변수(explanatory variable), 득점, 도움, 리바운드에 각각의 VIF를 계산한다.
그러기 위해서 하나의 변수를 반응 변수로, 나머지 2개의 변수를 원인 변수로 한 회귀분석을 한다. 예를 들어 득점을 반응 변수(reponse variable)로 하면 도움과 리바운드를 원인 변수(explanatory variable)로 한다.
그러면 이렇게 프린팅 된다.
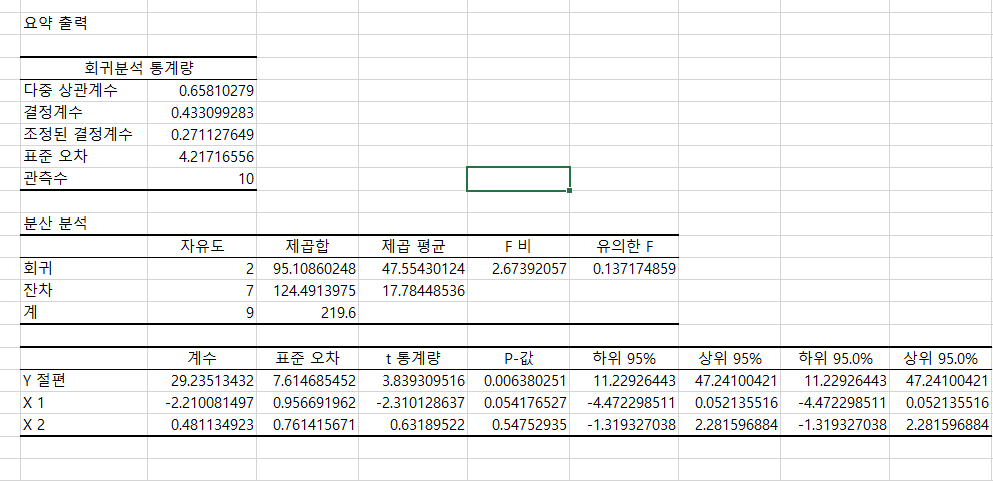
VIF = 1 / (1- R²)
여기서 결정계수는 0.4331이다.
VIF = 1/(1-0.4331) = 1.76
도움과, 리바운드에 대해 똑같은 분석을 반복 시행한다.
- 득점: 1.76
- 도움: 1.96
- 리바운드: 1.18
해석하기
VIF 값은 항상 1보다 크며, 상한이 없다. VIF 값을 아래 방법으로 해석할 수 있다.
- VIF = 1 : 주어진 원인 변수와 그 외 변수들 사이에 상관성이 없다.
- 1 < VIF ≤ 5 : 주어진 원인 변수와 그 외 변수들 사이에 어느정도 상관성이 있다. 하지만 통계 분석에 영향을 줄 만큼 크지는 않다.
- VIF > 5 : 5보다 크다면, 원인 변수와 그외 변수들 간에 상당한 상관성이 있다. 그래서 이 경우 회귀 분석 모델의 계수와 p-값에 대해 신뢰할 수 없다.
예시에서 값은 모두 5 이하로, 여기서 득점, 도움, 리바운드 간에 상이한 상관성이 없다.
'Excel_데이터 > 회귀분석' 카테고리의 다른 글
| 엑셀에서 Breusch-Pagan 검정(Breusch-Pagan Test) 하기 (0) | 2021.05.25 |
|---|---|
| 엑셀에서 회귀분석 표준오차(Standard Error of Regression) 구하기 (0) | 2021.05.18 |
| 엑셀에서 표준화 잔차(Standardized Residuals) 구하기 (0) | 2021.05.13 |
| 엑셀에서 잔차도(Residual Plot) 그리기 (0) | 2021.05.12 |
| 엑셀에서 예측 구간(Prediction Interval) 구하기 (0) | 2021.05.11 |