이상 검정(binomial test)은 관측한 확률이 예상한 확률과 같은지 안 같은지 확인하는 데 사용한다.
예를들어, 주사위를 24번 던졌다. 1/6의 확률로 3이 4번 나올 것이라 예상했다. 그런데 실제로 3이 6번 나왔다. 그렇다면 이 주사위는 3이 더 많이 나오도록 편중되어 있는 것일까??
위 질문에 이상검정(binomial test)을 통해서 답을 할 수 있다.
엑셀에서, 이상 검정(binomial은 엑셀에 내장 함수(built-in function)를 이용해서 쉽게 구할 수 있다.
BINOM.DIST(number_s, trials, probability_s, cumulative)
- number_s: 성공한 횟수
- trials: 전체 시도한 횟수
- probability_s: 각 시행마다 성공할 확률
- cumulative: True로 하면 누적 분포 함수(cumulative distribution function)를 반환한다. False로 하면 확률함수(Probability mass function)을 반환한다. 이상 검정(binomial test)에는 언제나 'True'로 한다.
이상검정(binomial test)을 몇 가지 예시로 실행해본다.
예시 1: 주사위를 24번 던진다. 3이 6번 나왔다. 주사위는 3번 많이 나오도록 만들어져 있는지 확인해본다.
귀무가설(null hypothesis)과 대립 가설(alternative hypothesis)을 설정한다.
- H0: π ≤ 1/6 (주사위는 3이 많이 나오도록 만들어지지 않았다.)
- HA: π > 1/6
*π는 '3'이 나올 확률이다.
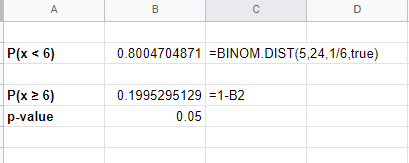
'3'이 6번보다 많이 나올 확률은 0.1995로 p-값 0.05보다 작지 않기 때문에 귀무가설(null hypothesis)을 기각할 수 없다. 그러므로 주사위가 '3'이 많이 나오도록 만들어졌다고 할만한 통계적 근거가 없다.
예시 2: 동전을 30번 던졌다. 그랬더니 19번 앞면이 나왔다. 이항 분석(binomial test)을 해서 동전이 원래 앞면이 많이 나오는지 검증해본다.
귀무가설(null hypothesis)과 대립 가설(alternative hypothesis)을 설정한다.
- H0: π ≤ 1/2 (동전은 앞면이 많이 나오도록 만들어지지 않았다.)
- HA: π > 1/2

'앞면'이 19번 보다 많이 나올 확률을 은0.10024로 p-값 0.05보다 작지 않기 때문에 귀무가설(null hypothesis)을 기각할 수 없다. 그러므로 동전이 '앞면'이 많이 나오도록 만들어졌다고 할만한 통계적 근거가 없다.
예시 3: 공장에 생산효율이 80%이다. 새로운 기계를 도입해서 효율을 올리려고 한다. 새로운 기계에서 생산된 50개의 상품들 중 46개가 불량이 없었다. 이상 검정(binomial test)을 통해서 효율이 올라갔는지 확인한다.
귀무가설(null hypothesis)과 대립 가설(alternative hypothesis)을 설정한다.
- H0: π ≤ 0.8 (새로운 기계는 생산성 향상이 없었다.)
- HA: π > 0.8

효율이 '0.8'보다 클 확률은 0.0184로 p-값 0.05보다 작기 때문에 귀무가설(null hypothesis)을 기각한다. 그러므로 새로운 기계가 효율이 개선했다고 볼 수 있다.
예시 4: 공장에서 생산효율이 60%이다. 새로운 기계를 도입해서 효율을 올리려고 한다. 새로운 기계에서 생산된 40개 상품을 임의로 추출했다. 얼마만큼 상품이 불량이 없어야지 신뢰구간(confidence level) 95%에서 효율이 올라갔다고 할 수 있을까?
상품을 숫자를 구하기 위해서 BINOM.INV(trials, probability_s, alpha) 함수를 사용한다.
- trials: 전체 시도 횟수
- probability_s: 각 시행마다 성공할 확률
- alpha: 신뢰 수준(여기서는 0.95)

최소 29개 이상의 상품이 나와야지 신뢰구간 95%에서 생산효율이 60%라고 할 수 있다.
'Excel_데이터 > 가설검증' 카테고리의 다른 글
| 엑셀에서 효과크기(Cohen's D) 구하기 (3) | 2021.04.20 |
|---|---|
| 엑셀에서 상관계수 검정(Correlation Test) 하기 (0) | 2021.04.19 |
| 엑셀에서 윌콕슨 부호순위 검정(Wilcoxon Signed Rank Test) 하기 (0) | 2021.04.17 |
| 엑셀에서 양비율 z-검정(Two Proportion Z-Test)하기 (0) | 2021.04.16 |
| 엑셀에서 단비율 z-검정(One Proportion Z-Test) 하기 (0) | 2021.04.16 |