palefaceman's digital repository

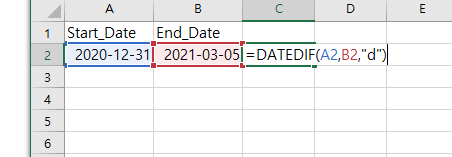
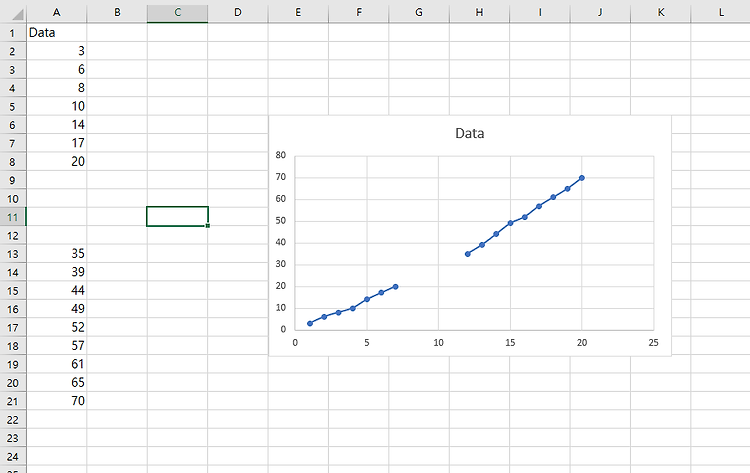
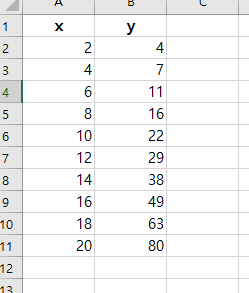
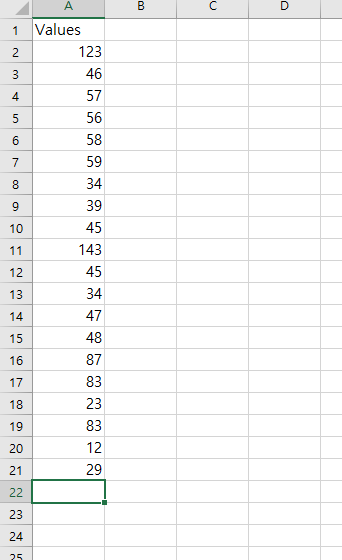
왜도(skewness)는 데이터 분포에 비대칭 정도를 보여주는 수치다. 값은 +또는-일 수 있다. 왜도(skewness)로 분포 모형을 유추하는데 도움이 된다. 왜도(skewness)의 -값은 꼬리가 왼쪽에 꼬리 넓이가 더 크다. 왜도(skewness)의 +값은 꼬리가 왼쪽에 꼬리 넓이가 더 크다. 왜도(skewness)의 0 값은 꼬리가 기울어짐 없이 평균값(mean)에 대칭이다. 구하는 법 =SKEW(array) 함수가 엑셀에 있다. 이 함수는 SKEWNESS = [n/(n-1)(n-2)] * Σ[(xi–x)/s]3 n = 표본 크기 Σ = 합 xi = i번째 데이터의 값 x = 평균 s = 표준편차 엑셀에서 위의 복잡한 식을 함수 하나로 간단하게 계산해준다. 예제 위의 표에서 왜도(skewness)..

변동 계수(CV, coefficient of variation)는 데이터의 퍼짐 정도와 데이터의 평균값에 관계를 나타낸다. CV= σ/μ σ = 표준편차(standard deviation) μ = 평균(mean) 위의 식에서 보면 변동 계수(CV, coffiecient of variation)는 수학 기호로 단순히 표준편차/평균값이다. 어디에 쓰이는가? 변동 계수(CV, coefficient of variation)는 두 데이터 간에 비교하는 데 사용된다. 이를테면 두 기대수익률 데이터에서 평균과 표준편차의 관계로 두 기대수익률을 비교하여 리스크 판단과 손절각을 결정하는 도구로 사용된다. A 펀드: 평균 7%, 표준편차= 12.4% B 펀드: 평균 5%, 표준편차 = 8.2% A펀드 CV: 12.4/7 ..

중간범위는=(제일 큰 값 +제일 작은 값)/2로 구한다 데이터에서 가장 큰 값과 가장 작은 값의 평균이다. 그리고 데이터의 중심이 어디에 위치해 있는지 알려준다. 이렇게 하면 중간값(midrange)은 24.5가 나온다. 중간범위(midrange) 단점 중간범위(midrange)는 outlier 값에 취약하다. 만약 위의 데이터 120이 포함되면 중간범위(midrange)는 60으로 데이터의 중심과 크게 떨어져 있다. 중간범위(midrange) 대안 중간범위(midrange)는 데이터에 중앙(center)을 구하는데 자주 사용되지 않는다. 그 이유는 outlier에 취약하지 않은 좋은 수단들이 많기 때문이다. 대표적으로 평균값(mean), 그리고 중앙값(median)이다. 이렇게 하면 중간범위(midra..

interquartile range(IQR)을 엑셀에서 구해보자. IQR(interquartile range)는 데이터에서 50% 구간에서 데이터가 '퍼져나간 정도'를 말해준다. IQR(interquartile range)는 Q3-Q1로 구해진다. IQR 숫자 자체로 특정한 의미를 가지지 않고, 크냐 작냐의 정도로 중앙값(median)에서 얼마나 데이터가 퍼져있는지를 알아볼 수 있는 척도(measure)이다. *Quartile은 데이터를 4개(Quarter)로 나눈 것이다. [58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98] 위의 데이터에서 Q3는 91이고 Q1는 75.5다. 그래서 IQR는 91 - 75.5 =..

평균(mean)은 데이터의 값들 중에 어디에 중간이 있을지 보여준다. 표준편차(standard deviation)는 데이터가 평균에 얼마나 밀접하게 분포되어 있는지 보여준다. 두 개의 값을 이용하면 데이터의 분포에 대해 한 눈에 알아볼 수 있다. =AVERAGE(ragne) =STDEVS.(range) STDEV()와 STEDV.S() 는 모두 표본집단에 대한 표준편차를 구해준다 그에 반해 STDEV.P()는 모집단에 대한 표준편차를 구한다. 하지만 대부분에 통계 데이터는 표본집단으로 하기 때문에 STDEV.P()는 사용하는 빈도수가 적다. 1. 평균 표준편차 구하기 위의 데이터에 대하 표준편차와 평균을 구할 수 있다. 평균은 16.4 표준편차 9.13으로 나온다. 2. 여러개의 데이터에서 평군 표준편차..

통계의 5개 상수를 구해보자 최솟값 Q1 중간값 Q3 최댓값 5개 상수는 이렇게 있다. 이 상수들은 굉장히 유용하다. 통계 데이터에 대한 전반적인 추론을 하도록 돕는 간략한 숫자로 사용된다. 데이터에 중간값에 대해 알려준다. Q1, Q3는 데이터에 '퍼짐'을 알려준다. 최대, 최솟값은 데이터에 범위를 알려준다. 위 5개 숫자로 데이터가 가지는 상당한 속성을 알아낼 수 있다. 어떻게 찾는가? 임의의 데이터에 값에서 옆에 함수를 이용하면 각각에 값을 구할 수 있다. 이렇게 하면 Minimum: 4 1st Quartile: 7.5 Median: 17 3rd Quartile: 22 Max: 28 이렇게 구할 수 있다. QUARTILE() 함수에는 몇 가지 종류가 있다. QUARTILE.INC()- 크거나, 같은..

Datedif() 함수를 이용해서 날짜 간의 차를 구할 수 있다. 사용 방법 =DATEDIF(Start_Date, End_Date, Metric) Start_Date: 시작 날짜 End_Date: 끝나는 날짜 Metric: 'd: 날', 'm: 달', 'y: 년' 엑셀에서 datedif()를 사용하려면 =DATEDIF( 까지 타입해야한다. 예시1: 날짜 차이 작년 12월 13일과 오늘까지는 64일 차가 있었다. 예시2: 달 차이 2달 예시3: 년 차이 0 년

가장 쉬운 법은 편지에서 채우기를 사용하는 것이다. 방법 1: 홈> 편집> 채우기> 계열 계열로 정리하게 하면 엑셀은 스텝 = (end-start)/(#miisng obs+1) (35-20)/(4+1) = 3으로 데이터를 채운다. 방법 2: 급수로 채우기 이렇게 나와있는 그래프가 있다. 급수로 채운다. 채운다. 이때 Trend(추세)는 취소한다. 이렇게 넣으면 자연스러운 그래프를 그린다.

예시: Linear Interpolation in Excel 이렇게 데이터 시트를 작성하고 그래프로 뽑아낸다. 만약에 x 13값에 대한 y(13)을 알고 싶다면 어떻게 해야하나? =FORECAST(NewX,OFFSET(KnownY,MATCH(NewX,KnownX,1)-1,0,2), OFFSET(KnownX,MATCH(NewX,KnownX,1)-1,0,2)) 이렇게 함수를 실행하면 33.5라는 값이 나온다. 그리고 기존 데이터에 (13,33.5)를 입력해보면 위에서 보듯이 기존 그래프에 정확하게 들어간다.

데이터에서 상위 10 값을 찾아야 할 때가 있다. 2가지 방법으로 찾아보자. Large() 함수를 쓰면 쉽게 할 수 있다. Large(array, k) array: 범위 k: 범위 안에서 k 번째로 큰 값 어떻게 쓰는지 보도록 하자 1. 조건부 함수 > 상/하위 규칙 > 상위 10% 상위 값 10개를 찾기 위해 새로운 열 k를 생성하고 1~10까지 입력한다. 그 옆에 새로운 열 Value를 생성하고 =LARGE($A$2:$A$21, C3) 입력한다. 아래 행까지 똑같이 실행한다. 상위 1개의 값은 옆에서 처럼 142~48까지다.