대응표본 t-검정(paired samples t-Test)은 같은 표본이 다른 조건에서 시행되었을 때 평균값(mean)을 비교하는 검정으로 쓰인다.
대응표본 t-검정(paired samples t-Test)을 해본다.
엑셀에서 대응표본 t-검정(paired samples t-Test)하기
어떤 화학반응의 25℃와 100℃에서 수율(yield) 차이를 알아보려고 한다. 그래서 25℃에서 실험을 20개의 샘플로 실시하고 같은 방법으로 100℃에서 20개의 샘플 실험을 실시하였다.
두 실험 결과의 평균을 비교하기 위해서 대응표본 t-검정(paired samples t-Test)을 시행하였다.
아래 실험의 수율(yield)이 나왔다.
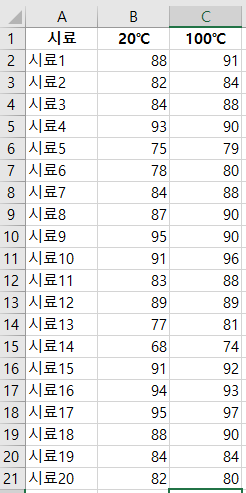
대응표본 t-Test(paired samples t-test)을 단계별로 진행하면서, 두 표본의 평균이 같은지 다른지 판별해 본다.
1단계: 데이터 분석 툴을 연다.

데이터 분석에 들어간다. 데이터 분석 툴이 없다면 여기서 확인한다.
2단계: 대응표본 t-test(paired samples t-test)를 선택한다.

대응표본 t-test(t-검정: 쌍체비교)를 클릭한다.
3단계: 필요한 정보를 입력한다.
- 변수 1: B2:B21
- 변수 2: C2:C21
- 유의 수준: 0.05
출력 범위를 원하는 곳에 지정한다.

4단계: 결과를 해석한다.
확인을 누르면 결과가 나온다.

- 평균(mean): 변수1의 평균 85.4, 변수2의 평균 87.2
- 분산(variance): 변수 1의 분산 51.51, 변수2의 분산 36.06
- 관측수(Observation): 변수1과 변수 2의 크기 20
- 피어슨 상관계수(Pearson Correlation): 20℃와 100℃에서 시료 수율(yield)의 상관관계(correlation) 0.9187
- 가설 평균차(Hypothesized mean difference): 귀무 가설(null hypothesis)에서 가정한 평균의 차이 '0'
- 자유도(degrees of freedom): n1+n2-2 =19
- t 통계량(t statistics): t-검정에 t 통계량 -2.78
- P(T<=t) 양측 검정(two tail): t 통계량에서 찾은 p-값이다. 자유도 19와, 유의 수준 0.05에서 p-값이다. p-값은 0.011907이다. 이는 알파값 0.05보다 작다. 그러므로 귀무가설(null hypothesis)을 기각한다. 두 실험 결과의 평균은 유의 수준 0.05에서 통계적으로 같지 않다고 할 수 근거가 있다.
- t 기각치 양측 검정(t critical two-tail): t 분포 테이블에서 찾은 자유도 19, 유의수준 0.05 양측 검정 t 기각치(t critical value)이다. 이 값은 2.093024다. t-검정에 t 통계량(t statistics)의 절댓값은 2.78094로 t 기각치(t critical value)보다 크다. 그러므로 귀무가설(null hypothesis)을 기각한다. 두 실험 결과의 평균은 유의 수준 0.05에서 통계적으로 같지 않다고 할 근거가 있다.
p-값과, t 기각치(t critical value)에서 같은 결과로 나왔다.
'Excel_데이터 > 가설검증' 카테고리의 다른 글
| 엑셀에서 맥니마 검정(McNemar's Test) 하기 (0) | 2021.04.15 |
|---|---|
| 엑셀에서 그럽스 검정(Grubbs' Test) 하기 (0) | 2021.04.15 |
| 엑셀에서 웰치의 t-검정(Welch's t-Test)하기 (0) | 2021.04.10 |
| 엑셀에서 2표본 t-검정(Two Sample t-Test)하기 (1) | 2021.04.09 |
| 엑셀에서 단일표본 t-검정(One Sample t-Test) 하기 (0) | 2021.04.06 |