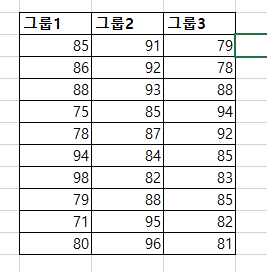
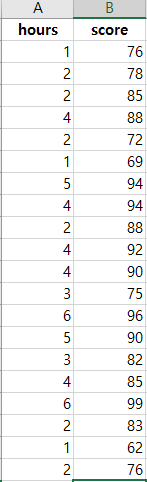
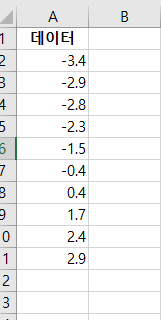
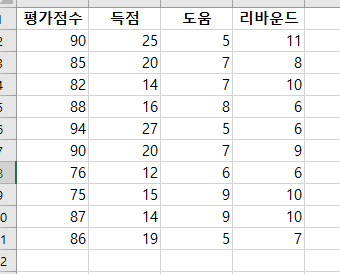
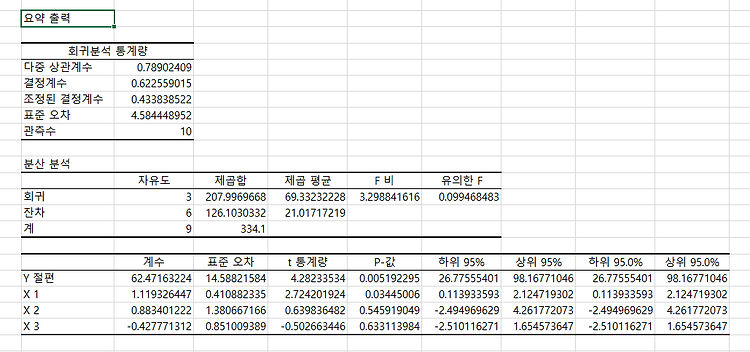
단 방향 ANOVA(one-way ANOVA)는 3개 이상의 독립적인 그룹의 평균 간에 유의미한 차이가 있는지 판별하는 검정 방법이다. 단 방향 ANOVA(one-way ANOVA)에서 사용된 가설은 귀무가설(null hypothesis), H0: μ1= μ2=μ3=...=μk (각각 그룹에 평균은 같다.)이다. 대립 가설(alternative hypothesis), Ha: 적어도 하나의 평균의 값이 다르다, 이다. ANOVA에서 구해진 p-value가 유의 수준(siginificance level)보다 작으면, 귀무가설(null hypothesis)을 기각할 수 있다. 그리고, 적어도 하나의 평균이 다르다고 볼 수 있는 충분한 통계적 근거가 있다고 말할 수 있다. 그러나, ANOVA로 어느 그룹에 평균..