포아송 분포(Poisson distribution)는 통계에서 많이 쓰이는 분포이다.
엑셀에서 POISSON.DIST() 함수로 주어진 시간(Time-Interval) 동안 사건(event)이 일어나는 평균 횟수를 알고 있는 사건(event)에 대해서, 주어진 시간 동안(interval) 사건(event)이 몇 번이나 일어날지에 대한 확률을 구할 수 있다.
POISSON.DIST(x, mean, cumulative)
- x: 주어진 시간동안 사건이 일어나는 횟수
- mean: 주어진 시간동안 사건이 일어나는 평균 횟수
- cumulative: TRUE는 누적확률을 반환, FALSE는 일어날 확률 반환
몇 가지 예시를 본다.
예시 1
자동차 딜러 A 씨는 한 달에 평균 3대의 차를 판다. A시가 한 달에 5대를 팔 확률은 얼마일까?
POISSON.DIST(x, mean, cumulative)
- x: 한 달에 5대를 판다.
- mean: 한 달 평균 3대를 판다.
- cumulative: FALSE (누적확률 X, 정확한 확률 값 O)

A 씨가 한 달에 5대를 판매할 확률은 0.10819이다.
예시 2
고양이 잡화 B에서 하루에 평균 15개의 츄르를 판다. 고양이 잡화B에서 하루에 츄르를 20개보다 더 많이 팔 확률은 얼마 인가?
POISSON.DIST(x, mean, cumulative)
- x: 하루에 20개 이상
- mean: 하루 평균 15개 츄르 판매
- cumulative: FALSE (누적확률 O, 정확한 확률 값 X)

고양이 잡화B에서 하루에 20개 이상을 판매할 확률은 0.082971이다.
※ POISSON.DIST(20,15, TRUE)에서 20개 이하일 때 확률을 반환한다. 전체 확률(1)에서 POISSON.DIST(20,15, TRUE)의 값을 빼면 20 보다 더 많은 츄르를 팔 확률이 나온다.
예시 3
헬스 트레이너 C 씨는 하루 평균 7명의 회원을 PT 한다. C 씨가 하루에 4명 이하를 PT 할 확률은 얼마 일까?
POISSON.DIST(x, mean, cumulative)
- x: 하루에 4명 이하
- mean: 하루 평균 7명 PT
- cumulative: FALSE (누적확률 O, 정확한 확률 값 X)
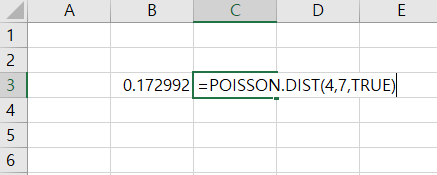
헬스 트리 레이너 C 씨가 하루에 4명 이하를 PT 할 확률은 0.172992다.
예시 4
수험생 D 씨는 하루 평균 12시간 공부를 한다. D 씨가 하루에 12-14시간 공부할 확률은?
POISSON.DIST(x, mean, cumulative)
- x: 하루에 12-14시간 공부
- mean: 하루 평균 12시간 공부
- cumulative: FALSE (누적확률 O, 정확한 확률 값 X)

수험생 D씨가 하루에 12-14시간 공부할 확률은 0.310427이다.
※
1. POISSON.DIST(14,12, TRUE): 0에서 14시간 확률을 반환
2. POISSON.DIST(11,12, TRUE): 0에서 11시간 확률을 반환
1-2를 하면 14,13,12시간을 공부할 확률, 12-14시간 공부할 누적확률이 나온다.
또 다른 방법은 12,13,14 시간을 공부할 확률을 각각 구하고, 세 값을 합한다.

같은 값을 반환한다.
'Excel_데이터 > 확률분포' 카테고리의 다른 글
| 엑셀에서 균일분포(Uniform Distribution)구하기 (0) | 2021.04.01 |
|---|---|
| 엑셀에서 삼각분포(Triangular Distribution) 구하기 (0) | 2021.04.01 |
| 엑셀에서 이항분포(binomial distribution) 구하기 (0) | 2021.03.31 |
| 엑셀에서 경험 법칙(Empirical Rule) 적용하기. (0) | 2021.03.30 |
| 엑셀에서 t-분포(t-distribution) 그래프 그리기 (0) | 2021.03.30 |