palefaceman's digital repository

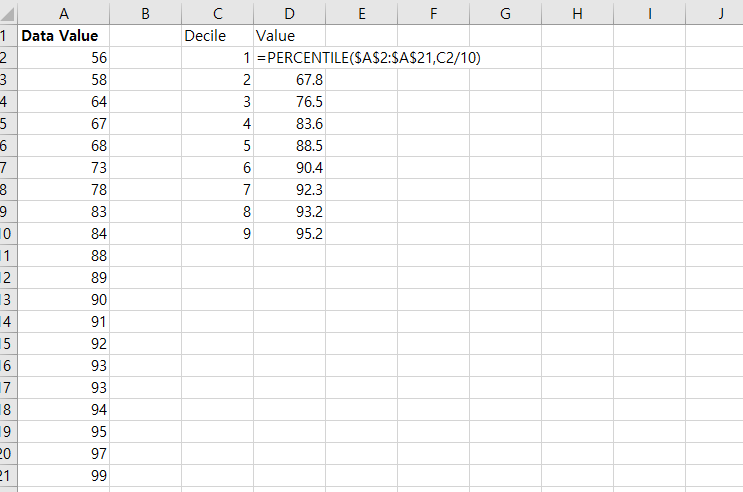
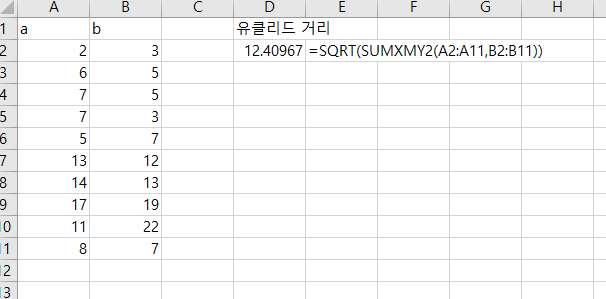
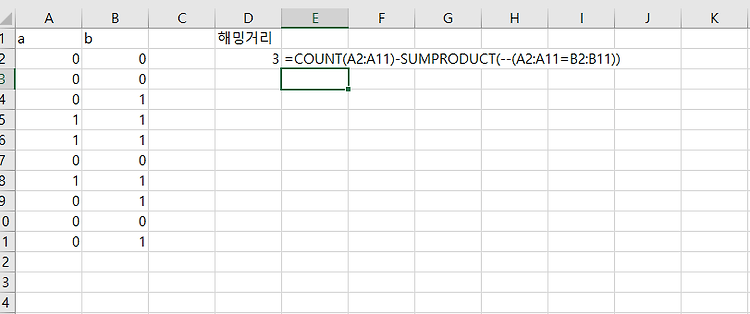
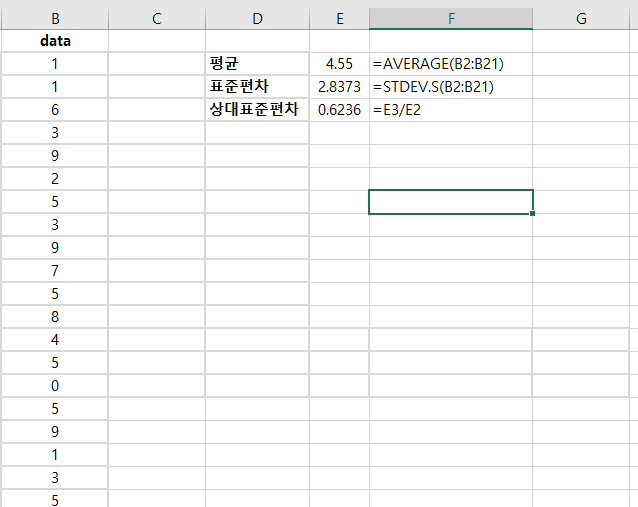
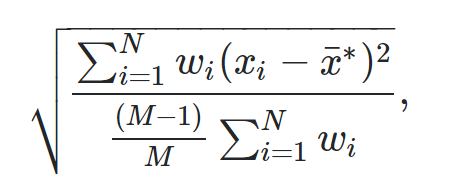합동 분산(pooled variance)은 두 개 이상의 데이터 표본(sample)의 분산에 평균을 한 통계 지표다. 합동 분산(pooled variance)은 두 개 이상의 데이터 표본(sample)의 분산(variance)을 통합해서 공용 하나의 분산(variance)를 의미한다. 합동 분산(pooled variance)은 두 표본(two samples)에 대한, t-test를 할 때 가장 많이 사용된다. (t-test는 표본의 평균이 같은지 아닌지 측정하는 테스트) 합동 분산(pooled variance)는 sp^2 기호로 사용된다. sp^2 = ( (n₁-1)s₁^2 + (n₂-1) s₂^2 ) / (n₁+n₂-2) 어떻게 구하는지 살펴본다. 1단계: 데이터 생성 2단계: 표본크기(sample s..

가중 표준편차(weighted standard deviation)는 일부 데이터에 더 가중을 둬서 데이터의 분산(dispersion)을 구하는 방법이다. 가중 표준편차(weighted standard deviation)를 구하는 방법은 이렇다. N: 전체 관찰값의 크기 M: 가중치가 0이 아닌 가중치 수 wi: i번째 관찰값의 가중치 xi: i번째 데이터 값 x: 가중치 평균 가중표준편차(weighted standard deivation)를 단계별로 구해보자 1단계: 데이터 생성 2단계: 가중 평균 계산 =SUMPRODUCT(A2:A11,B2:B11)/SUM(B2:B11) 가중치 평균(Weighted Mean)은 31.147 3단계: 가중 표준편차(Weighed Standard Deviation) 구하기..

각기 다른 계급에서 매겨진 개수가 같이 쓰일 수 있는지 알아보는 통계지표가 급내상관계수(Interclass Correlation Coefficients, ICC)이다. ICC(급내상관계수)는 0에서 1 범위에 값이다. 0은 계급간 상관관계없음, 1은 계급관 완벽하게 상관관계있음 어떻게 구하는지 살펴보자 1단계: 데이터 생성 각각의 시험 10 과목에 대해 4명의 심사자가 점수를 매긴 현황 데이터다. 2단계: ANOVA 분산 분석하기 ANOVA 분산분석을 하기 위해서 데이터> 데이터 분석> 분산분석: 반복 없는 이원 배치법에 들어간다. 그리고 아래에 같이 세팅을 마치고 확인한다. 결과는 이와 같다. 3단계: ICC(급내상관계수)를 구한다. 분산분석을 통해 나온 A행, B열의 자유도와, 제곱 평균, 잔차의 제..

생물통계학자 Karl Pearson에 의해 고안된 통계지표가 피어슨 비대칭계수(Pearson's Coefficient of Skewness)다. 피어슨 비대칭계수(Pearson's Coefficient of Skewness)는 왜도(Skewness)를 측정하는데 용이하다. 피어슨 비대칭계수(Pearson's Coefficient of Skewness)를 구하는 두 가지 방법이 아래에 있다. 방법 1: 최빈수(mode) 이용하기 왜도(skewnesss) = (평균 - 최빈수)/표본 표준편차 방법 2: 중앙값(median) 이용하기 왜도(skewnesss) = 3*(평균 - 중앙값)/표본 표준편차 방법 1보다 방법 2가 더 많이 사용된다. 최빈수(mode)는 데이터에 중앙(the center of data)..

윈저화(winsorization)은 이상치(outlier)를 처리하는 기법으로 이상치를 특정 백분위수(percentile)에 값으로 치환해버린다. 예를 들어 90% 윈저화(winsorization)을 하게 되면 95 번째 값보다 큰 데이터는 모두 95 번째 데이터로 치환한다. 또는 5 번째 데이터 값보다 낮은 데이터는 모두 5 번째 데이터로 치환한다. 어떻게 하는지 예시를 보자 1단계: 데이터 셋팅 2단계: 5%,95% 백분위수 구하기 PERCENTILE(array, k) 함수를 이용해서 5 째, 95 쨰 백분위수를 구해준다. 5% 백분위수 12.35 95% 백분위수 92.05 3단계: 윈저화(Winsorization) 한다. IF(Condition, True, False) 함수로 크거나 작거나, 조건을..

PROB() 함수를 이용해서 엑셀에서 확률을 구할 수 있다. PROB(x_range, prob_range, lower_limit, [upper_limit]) x_range: x의 범위 prob_range: 확률의 범위 lower_limit: 확률을 알고 싶은 최소 범위 upper_limit: 확률을 알고 싶은 최고 범위 사용 예시를 살펴보자 예시 1: 주사위 확률 아래에 주사위 나올 확률표가 있다. 주사위의 각면에 나올 확률이 동일하여 같은 값을 가진다. 여기서 PROB()함수로 4에서 6이 나올 확률을 구해본다. 예시 2: 판매 확률 다음은 회사에서 판매하는 상품이 팔릴 확률이다. 3이나 4가 팔릴 확률을 구해보자

통계에서 Decile은 데이터를 10단계로 그룹화는 것을 말한다. 첫 번째 Decile은 아래에서 10%의 데이터 값을 포함한다. 두 번째 Decile은 아래에서 20%의 데이터 값을 포함한다. =PERCENTILE(CELL RANGE, PERCENTILE) 위의 함수로 Decile을 구할 수 있다. cell range에 데이터 array를 넣고, percentile에 원하는 %를 넣는다. 예시 1: 20%에 데이터는 67.8 아래에 있다. 30%에 데이터는 76.5 아래에 있다. 40%에 데이터는 83.6 아래에 있다. 각각의 데이터의 decile에 넣기 위해서 PERCENTILERANK.EXC() 함수를 사용한다. =PERCENTRANK.EXC(CELL RANGE, DATA VALUE, SIGNIFI..

두 벡터 간 유클리디안 거리(Euclidean distane)는 다음과 같이 나타낸다. Euclidean distance = √Σ(Ai-Bi) 2 Σ: 합계 Ai: A벡터의 i번째 요소의 값 Bi: B벡터의 i번째 요소의 값 엑셀에서는 함수들을 이용해서 구할 수 있다. =SQRT(SUMXMY2(RANGE1, RANGE2)) SUMXMY2: range1과 range2의 각각의 요소들에 차에 제곱을 구해준다. SQRT: 루트(root)를 씌워준다. 유클리드 거리는 12.40967이다. 유클리드 거리는 반드시 대칭되는 두 배열(array), 범위(ragne), 벡터(vector), 크기(size)끼리만 적용된다. 예를 들어 이 두 차원이 다른 a, b 사이에 유클리드 거리는 성립되지 않는다.

해밍 거리(hamming distance)는 단순하게 두 벡터 간에 공통된 값(element)들의 개수에 합이다. x = [1, 2, 3, 4] y = [1, 2, 5, 7] 에서 해밍거리(hamming distance)는 '2'다. =COUNT(RANGE1)-SUMPRODUCT(--(RANGE1 = RANGE2)) 엑셀에서 해밍거리(hamming distance)는 이렇게 구한다. COUNT: 첫 번째 행에 갯수를 구한다.(행열의 크기) RANGE1 = RANGE2 각각의 열을 비교하여 TRUE or FALSE로 반환(return)한다. – – TRUE and FALSE 값을 0 and 1로 전환한다. SUMPRODUCT: 매칭되는 값(element)끼리 곱한다. 예시: 두 이진수 벡터 간 해밍 거리(..

상대표준편차(Relatie Standard Deviation)는 표본 집단(Sample)의 평균(mean)에 대비해서 표본의 표준편차(Standard Deviation)을 측정한다. 상대표준편차(Relative standard deviation) = s / x * 100% s: 표본 표준편차 x: 표본 평균 상대표준편차(Relative standard deviation)로 데이터값들이 평균(mean)에 얼마만큼 밀집되어 있는지 볼 수 있다. 예를들어 표준편차 4, 평균 400이면, 상대표준편차(relative standard deviation)은 4/400*100% = 1%다. 이 수치가 작으면 작을 수록 더 평균에 값들이 밀집해있다. 만약, 표준편차 40, 평균 400이면, 상대표준편차(relative..