palefaceman's digital repository

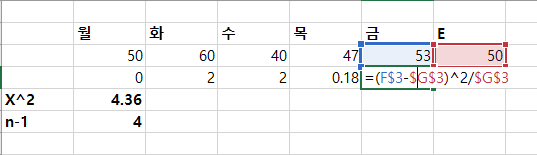
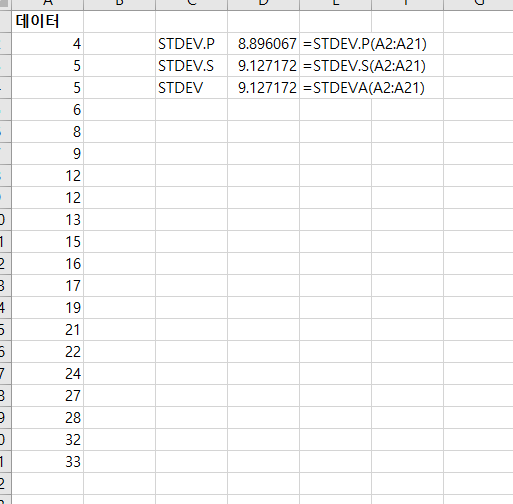
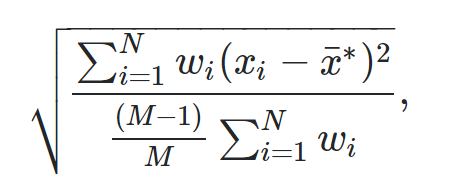z-점수(z-score)는 통계 데이터 값이 평균에서 얼마에 표준편차만큼 떨어져 있는지 보여주는 지표다. 백분위(percentile)는 관찰 값이 100으로 쪼겠을 때 어디에 분포하는지 보여주는 통계 지표다. 엑셀에 내장된 함수를 이용하면 쉽게 백분위와 z-점수간에 치환이 가능하다. z-점수를 백분위로 치환하기 =NORM.S.DIST(z, cumulative) z = 구하는 값에 z-점수(z-score) cumulative = TRUE 누적 분포 함수(cumulative distribution function); FALSE 확률분포 함수(Probability distribution Function). True로 한다. z-점수 1.78은 백분위로 0.9624와 같다. z-점수 1.78을 갖는 데이터 값은..

통계분석의 가설검정(hypothesis test)를해서 t-점수(t-socre)를 구하고 거기에 적합한 p-value를 구한다. 여기서 구한 p-value가 (0.10,0.05,0.01)등 특정 신뢰구간(confident interval) 보다 작으면 null 가설(null hypothesis)을 기각하고 그리고 가정(hypothesis)이 타당했다고 통계적 판단을 내릴 수 있다. 엑셀을 이용해서 t-점수에 p-value를 구해본다. T.DIST(x, deg_freedom) x: 검정을 할 t-점수 deg_freedom: 자유도 예시1: t-점수로 p-value 구하기(two-tailed) 어느 식물학자는 자기가 연구하는 한 식물종의 평균 크기가 15 cm인지 알고 싶다. 그래서 12개의 식물 표본을 채..

카이제곱 검정(Chi-Square Test)을 하게 되면 언제나 카이제곱 통계량(Chi-Square statistic)을 구하고 카이제곱 값을 기각할지 말지 p-value를 찾는다. 엑셀에서 카이제곱검정(Chi-Square Test)에 적합한 p-value를 찾기 위해 CHISQ.DIST.RT() 함수를 사용할 수 있다. =CHISQ.DIST.RT(x, deg_freedom) x: 카이제곱 값 deg_freedom: 자유도 아래 예시에서 실행해 본다. 예시1: 카이제곱 적합도 검정(Chi-Square Goodness of fit Test) 한 PC방 주인이 매일 똑같은 수에 손님이 온다고 했다. 이 가정을 검정해보자. 일주일간 온 손님 수를 관찰했다. 월 화 수 목 금 50 60 40 47 53 H0(n..

F-test는 F-통계량을 생성한다. p-value는 F-통계량과 관련돼있다. =F.DIST.RT(x, degree_freedom1, degree_freedom2) x: F-통계량 값 degree_freedom1: 분자 자유도 degree_freedom2: 분모 자유도 F-통계량에서 p-value를 구해본다. F-통계량 5.4, 분자 자유도 2, 분모 자유도 9이다. p-value는 0.02878이다. F-통계량은 회귀모델(regression model)에서 가장 흔히 쓰인다. 회귀모델(regression model)에서 p-value를 구해본다. 예: F-통계량에서 p-value 구하기 위의 데이터에 대해 데이터> 데이터 분석> 회귀분석을 실시한다. X -공부시간, 시험 Y - 점수 F-통계량은 5.0..

z-점수(z-score)는 표준편차를 기준으로 데이터가 평균에서 얼마만큼 떨어져 있나를 보여주는 통계지표다. z = (X – μ) / σ X: 데이터 값 μ: 평균 σ: 표준편차 엑셀에서 z-점수(z-score)를 구해본다. 엑셀에서 z-점수(z-score)구하기 아래에 데이터에서 모든 값에 대해 z-점수(z-score)를 구해보자 1단계: 평균과 표준편차 찾기 평균은 14.375 표준편차는 5.162 2단계: z-점수(z-score) 찾기 z = (X – μ) / σ 공식을 이용해서 z-점수(z-score)를 찾고 드래그로 칸을 채운다. z-점수(z-score) 판단하기 z-점수(z-score)는 값이 평균에서 표준편차를 단위로 얼마나 떨어져 있나를 지시한다.-값은 평균보다 뒤에, +값은 평균보다 앞에..

표본 분포(sampling distribution)는 모집단으로부터 추출된 n개의 표본(sample)들의 통계 값을 나타내는 것이다. 엑셀에서 어떻게 표본 분포(sampling distrubtion)를 구하는지 실습해본다. 데이터 추출 시각화하기 표본 데이터의 평균, 표준편차 구하기 확률 구하기 데이터 추출 =NORM.INV(RAND(), 5.3, 9) =NORM.INV(RAND(), 5.3, 9)을 사용해서 평균 5.3, 표준편차 9인 정규분포 모집단(population) 임의의 데이터를 추출해온다. 표본의 크기는 20, 추출 표본의 개수는 1000개로 한다. 이제 각셀에 평균을 구한다. 표본의 평균의 평균과 표준편차를 구한다. 표본 평균의 평균 5.424 표본 평균의 표준편차 2.0147 표준편차는 ..

중심 극한 정리(Central Limit Theorem)는 표본의 크기(n)이 충분히 크다면 표본의 분포가 정규화(normalization)된다는 가정이다. 심지어 모집단(population)이 정규분포(normal distribution)를 취하지 않더라도, 채취한 표본은 정규화(normalization) 된다. 중심 극한 정리(central limit theorem)는 또한 이와 같은 뜻을 가진다. 1. 표본의 평균은 모집단의 평균과 같다. x = μ 2. 표본의 표준편차는 모집단의 표준편차에 표본의 크기로 나눈 값과 같다. s = σ / √n 어떻게 엑셀에서 구하는지 알아본다. 중심 극한 정리(central limit theorem) 엑셀에서 구하기 어느 모집단 평균8, 표준편차 4를 가진다. 여기..

엑셀에서 표준편차(standard deviation)를 구하는 여러 가지 함수를 소개한다. 1.STDEV.P 모집단의 표준편차를 계산한다. 데이터 범위가 전체 모집단으로 할 때 사용한다. √Σ (xi – μ)^2 / N Σ: 합계 xi: i번째 데이터 값 μ: 모집단 평균 N: 관찰 개수(전체 데이터 크기) 2. STDEV.S 표본집단의 표준편차를 계산한다. 데이터 범위가 전체 모집단에서 채취한 표본집단일 때 사용한다. √Σ (xi – x)^2 / (n-1) Σ: 합계 xi: i번째 데이터 값 x: 표본 평균 n: 관찰 개수(전체 데이터 크기) 3.STDEV 표본집단의 표준편차를 계산한다. STEDV.S와 똑같은 값을 반환한다. Note 표본의 표준편차에서 N 대신 n-1을 사용한다. 표본의 크기는 항상..

합동 분산(pooled variance)은 두 개 이상의 데이터 표본(sample)의 분산에 평균을 한 통계 지표다. 합동 분산(pooled variance)은 두 개 이상의 데이터 표본(sample)의 분산(variance)을 통합해서 공용 하나의 분산(variance)를 의미한다. 합동 분산(pooled variance)은 두 표본(two samples)에 대한, t-test를 할 때 가장 많이 사용된다. (t-test는 표본의 평균이 같은지 아닌지 측정하는 테스트) 합동 분산(pooled variance)는 sp^2 기호로 사용된다. sp^2 = ( (n₁-1)s₁^2 + (n₂-1) s₂^2 ) / (n₁+n₂-2) 어떻게 구하는지 살펴본다. 1단계: 데이터 생성 2단계: 표본크기(sample s..

가중 표준편차(weighted standard deviation)는 일부 데이터에 더 가중을 둬서 데이터의 분산(dispersion)을 구하는 방법이다. 가중 표준편차(weighted standard deviation)를 구하는 방법은 이렇다. N: 전체 관찰값의 크기 M: 가중치가 0이 아닌 가중치 수 wi: i번째 관찰값의 가중치 xi: i번째 데이터 값 x: 가중치 평균 가중표준편차(weighted standard deivation)를 단계별로 구해보자 1단계: 데이터 생성 2단계: 가중 평균 계산 =SUMPRODUCT(A2:A11,B2:B11)/SUM(B2:B11) 가중치 평균(Weighted Mean)은 31.147 3단계: 가중 표준편차(Weighed Standard Deviation) 구하기..